Polymorphism is a great thing. .NET, Java, C++ and other folks have enjoyed its benefits for a long time, some more than a quarter century already. Meanwhile, we, the meager C/AL bunch, can only dream about it and draft our little patterns that all come short of it if only by a tiny bit.
Sometimes it feels like writing code with a chalk on a blackboard. There may be no end to your imagination, but there is a very real end to what the board can do for you.
But dream we can. And let me have another dream.
Why do I care so much about polymorphism, what’s so important in it that I’ve spent three blog posts talking about it, and then am dreaming out loud another one, only before I write a yet another one?
Well, in all honesty, I couldn’t care less about polymorphism itself. It’s just another programming concept. What I do care about is the things it can do for us.
In the old days, when there was on-prem only, even if polymorphism existed, it would not have been more than a architectural stunt, a trick to write our CASEs and IFs in a more elegant way.
But with Dynamics 365, with apps, and even only with extensions running in multi-tenant scenarios self-hosted by partners, polymorphism can achieve far more than offer some fun to programmers.
How’s that? Well, consider the past three post I wrote and the problem that we find buried deep down, every single time, no matter what angle we take, how far we dig, or how clever we attempt to be: either we have a sort-of-a-polymorphism at the cost of statelessness (and possibly some more); or we have statefulness at the cost of tight coupling on the far end of the façade in charge of loose coupling. No matter what you do, no matter how you approach it, this is what you get in the end.
However, one object type, which wouldn’t be that crazy difficult to add to the C/AL stack, would solve it all: CodeunitRef.
What would a CodeunitRef be? Well, think of RecordRef. You know what it is? Well, a CodeunitRef is the same, only for codeunits.
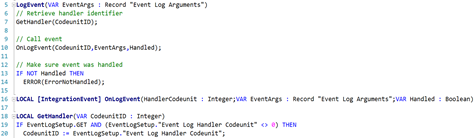
Consider this piece of code:
You may recognize the “handled” façade codeunit from the previous post. It retrieves the codeunit ID for the codeunit that should be in charge of handling the event, and then passes that codeunit ID on to the event, hoping that there is a codeunit with that ID that will actually decide to execute the logic, and that there are no more codeunits that would feign to be the one being called, and then hoping that whoever decides to handle the event will set the Handled flag to true. Far too much hoping for my taste.
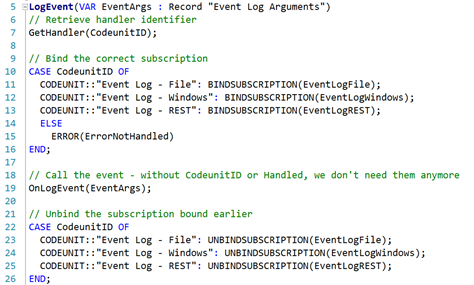
We could solve that in one fell swoop if only we could manually bind codeunit’s subscriptions, but to do that, we need an actual variable. The only way to solve it would be this:
This achieves the goal of having only the exact codeunit bound to the events, making sure only that codeunit executes the needed event. You also make sure that the bound codeunit retains its state (provided that somehow the façade codeunit does not go out of scope itself, losing the state – which can be solved in may different ways). You also achieve good separation of concerns: the actual event logger being called is only concerned with the business logic and doesn’t need to care about infrastructure; it’s the façade codeunit that takes care of it. There is no need to pass the identifier or the Handled flag into the event, because you know that there is only the correct handler bound to the event, and that it will execute.
However, you also provide hard coupling between the façade and the actual dependencies. This is bad because it requires changing code in and recompiling of the façade codeunit every time a new dependency type is added (say: Twitter logger codeunit). And every time you change and recompile the façade, for good measure you must at least recompile all the consumers, just to make sure you didn’t break anything.
With true loose coupling, or true polymorphism, you could add dependencies to the end of the world, without the need to touch or recompile anything.
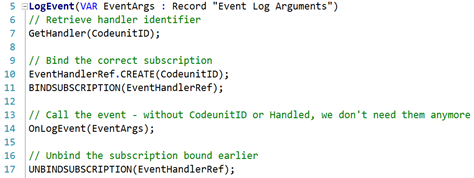
But, how do you like this:
I myself totally dig it, except for a little detail: it’s completely made up. It’s impossible.
What would make it possible is the CodeunitRef type in C/AL, variable EventHandlerRef being of CodeunitRef type.
As long as I maintain a living reference to the instance of the codeunit inside of this variable, that instance would be both alive and accessible, meaning that I would now be able to both retain the state, and access the codeunit without the need for a codeunit variable with an exact subtype. CodeunitRef variable would not have subtype: it would be able to change its subtype at runtime, much like RecordRef can do (okay, it doesn’t actually change subtype, but you know what I mean).
Much like we have FieldRef when handling RecordRef, we could also have FunctionRef when handling CodeunitRef. This is what, in fact, other languages call delegates.
Imagine this:
… and then this:
Once you have it, when you need to log events using whatever dependency is configured to handle it, you do this:
This stuff above, that I have just shown, is true inversion of control pattern executed using dependency injection (dependency injection is a manifestation pattern of the inversion of control pattern).
There is no end to what this could achieve. Maybe you don’t see it from this simple blog post, but dependency injection goes a long way in achieving different runtime behavior without compromising any other aspect of the logic being executed. Especially you don’t need to recompile anything or change anything.
What’s even more beautiful, when you need polymorphic behavior, you don’t need to use events. Events are great to simplify customization of the application, but using them to achieve loose coupling only introduces problems, more than it solves. Events should be used for zero-footprint changes of standard functionality, whereas dependency injection and inversion of control can be used to achieve loose coupling of dependencies in a robust, bulletproof way.
It’s not time to wake up just yet. CodeunitRef may be one way to solve the problem. I have proposed it because I believe it would be fairly simple to create. Just think of how much work it must have been for Microsoft to support .NET interoperability; I am pretty sure that CodeunitRef would feel like a Monday morning exercise as compared to that work.
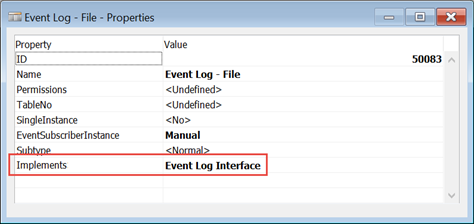
A more complicated way perhaps would be to implement another type instead of CodeunitRef: CodeunitInterface.
What that type would do is define the behavior of a codeunit by providing function signatures, without their implementation. Then, a codeunit could implement an interface like this:
Once you specify which interface(s) to implement, you’d need to provide exactly the same functions with exactly the same signatures. And once you do that, you could have a situation such as this:
… which you invoke like this:
What do you think of these suggestions? Would they make your life easier? Please, share your thoughts, I’d like to hear from you.
And now, time to wake up.




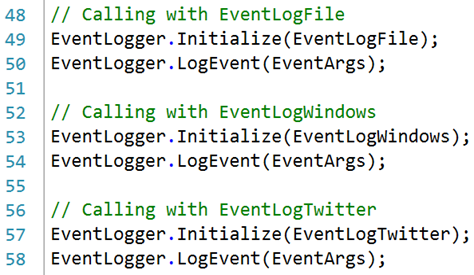


In my opinion, BINDSUBSCRIPTION, either on a Codeunit variable or on a CodeunitRef, does not solve one of the problems you are raising: the problem “that there are no more codeunits that would feign to be the one being called”.
It’s the subscriber Codeunit that defines the property EventSubscriberInstance, setting it to either Static-Automatic or Manual. It’s not the Event definition that specifies what type of subscriber can handle the event.
How do you prevent Static-Automatic subscriber Codeunits to handle the event that you try to specifically bind to a certain Codeunit instance?
As far as I can see, there is no way to prevent multiple subscribers to react to an event, the only benefit of BINDSUBSCRIPTION is that you can bind an existing instance (with its current state) of a Codeunit to a certain event.
If other Codeunits (Static-Automatic) subscribe to the same event, they will just be called, nothing that you can do to stop that.
Furthermore, the concept of CodeunitRefs to be instantiated so they can react on an event is close to instantiate a CodeunitRef and call a function in it, because you know it’s interface. So, in my opinion, the idea of having interfaces with Codeunits is a better way to solve the problems you are raising here. Only then you know for sure that the Codeunit you are calling, and only that single Codeunit instance, will handle your event (which is not an event anymore, but a loosly coupled function call).
Where exactly do we disagree? 🙂 By the way – there is a way to prevent a static-automatic codeunit to handle the event. It’s not nice, but it exists (and you’ve seen it, and I’ll blog about it when I blog about the Module Binder pattern). As I said – events should not be used for situations where you need loose coupling. Events are broadcasts, loose coupling is something completely different. But essentially, I believe you and I agree here.
We are on the same page 🙂
Just wanted to point out that manual subscribers, not even with codeunit refs, are the solution for some of the problems you are raising.
True.
I really like the CodeunitInterface idea more than the CodeunitRef because it feels more “NAV-like” to me. CodeunitRef would be the more powerful concept but also more difficult to understand and maintain code while CodeunitInterface in my opinion would be quite straight forward. The code using CodeunitRef would be more efficient and elegant but I think in the long term and with bigger development teams where everyone needs to understand the code CodeunitInterface would be easier to handle.
But most of all I agree with you that Events definitely aren’t the way to implement loose coupling. Not sure if this translates well but there is a German figure of speech “if you hold a hammer, everything looks like a nail”. I hope MS is not feeling that way about Events 🙂
Thanks for sharing your thoughts. The “hammer and nail” analogy exists in many languages, and it hits the bulls eye here. We got events, and now suddenly everything has to be solved with events, and it’s certainly not so. They are the best hammer we had so far, but we still need a pincette…
Thanks for great post. After reading this post, I just couldn’t stop thinking about an idea of implementing FunctionRefs in NAV 2016. In the end NAV is just a .NET application and every object is just a .NET class, so I thought it should be possible and yes it is :). This is my proof of concept (while not perfect it works):
OBJECT Codeunit 50000 FunctionRef
{
OBJECT-PROPERTIES
{
Date=16.10.06;
Time=19:41:56;
Version List=;
}
PROPERTIES
{
OnRun=BEGIN
END;
}
CODE
{
VAR
ArgumentsList@1003 : DotNet “‘mscorlib, Version=4.0.0.0, Culture=neutral, PublicKeyToken=b77a5c561934e089’.System.Collections.Generic.List`1”;
CodeunitDotNetHandle@1002 : DotNet “‘Microsoft.Dynamics.Nav.Ncl, Version=9.0.0.0, Culture=neutral, PublicKeyToken=31bf3856ad364e35’.Microsoft.Dynamics.Nav.Runtime.NavCodeunit”;
CurrCodeunitId@1000 : Integer;
CurrFunctionName@1001 : Text;
PROCEDURE Create@1(CodeunitId@1000 : Integer;FunctionName@1001 : Text);
BEGIN
CurrCodeunitId := CodeunitId;
CurrFunctionName := FunctionName;
END;
PROCEDURE Invoke@3();
BEGIN
InitArgList;
InvokeActual;
END;
PROCEDURE Invoke1Arg@2(Arg1@1000 : Variant);
BEGIN
InitArgList;
AddArgument(Arg1);
InvokeActual;
END;
PROCEDURE Invoke2Arg@4(Arg1@1000 : Variant;Arg2@1001 : Variant);
BEGIN
InitArgList;
AddArgument(Arg1);
AddArgument(Arg2);
InvokeActual;
END;
PROCEDURE Invoke3Arg@5(Arg1@1001 : Variant;Arg2@1000 : Variant;Arg3@1002 : Variant);
BEGIN
InitArgList;
AddArgument(Arg1);
AddArgument(Arg2);
AddArgument(Arg3);
InvokeActual;
END;
PROCEDURE Invoke4Arg@6(Arg1@1001 : Variant;Arg2@1000 : Variant;Arg3@1002 : Variant;Arg4@1003 : Variant);
BEGIN
InitArgList;
AddArgument(Arg1);
AddArgument(Arg2);
AddArgument(Arg3);
AddArgument(Arg4);
InvokeActual;
END;
LOCAL PROCEDURE InvokeActual@10();
BEGIN
CodeunitDotNetHandle.Invoke(CurrCodeunitId, CurrFunctionName, ArgumentsList.ToArray);
END;
LOCAL PROCEDURE InitArgList@7();
BEGIN
ArgumentsList := ArgumentsList.List;
END;
LOCAL PROCEDURE AddArgument@8(Arg@1000 : Variant);
VAR
Date@1001 : Date;
BEGIN
//TODO: ok for Proof of concept, but need to think about other data types unboxing
IF Arg.ISDATE THEN
BEGIN
Date := Arg;
ArgumentsList.Add(Date);
END
ELSE
ArgumentsList.Add(Arg);
END;
BEGIN
END.
}
}
OBJECT Codeunit 50001 Implementation 1
{
OBJECT-PROPERTIES
{
Date=16.10.06;
Time=19:47:54;
Version List=;
}
PROPERTIES
{
OnRun=BEGIN
END;
}
CODE
{
PROCEDURE TestOne@1();
BEGIN
MESSAGE(‘Implementation 1’);
END;
PROCEDURE TestTwo@2(TestInt@1000 : Integer);
BEGIN
MESSAGE(‘Implementation 1, Arg1: %1’, TestInt);
END;
PROCEDURE TestThree@3(TestInt@1000 : Integer;TestDate@1001 : Date);
BEGIN
MESSAGE(‘Implementation 1, Arg1: %1, Arg2: %2’, TestInt, TestDate);
END;
BEGIN
END.
}
}
OBJECT Codeunit 50002 Implementation 2
{
OBJECT-PROPERTIES
{
Date=16.10.06;
Time=19:48:19;
Version List=;
}
PROPERTIES
{
OnRun=BEGIN
END;
}
CODE
{
PROCEDURE TestOne@1();
BEGIN
MESSAGE(‘Implementation 2’);
END;
PROCEDURE TestTwo@2(TestInt@1000 : Integer);
BEGIN
MESSAGE(‘Implementation 2, Arg1: %1’, TestInt);
END;
PROCEDURE TestThree@3(TestInt@1000 : Integer;TestDate@1001 : Date);
BEGIN
MESSAGE(‘Implementation 2, Arg1: %1, Arg2: %2’, TestInt, TestDate);
END;
BEGIN
END.
}
}
OBJECT Codeunit 50003 Test Proof of Concept
{
OBJECT-PROPERTIES
{
Date=16.10.06;
Time=19:46:36;
Version List=;
}
PROPERTIES
{
OnRun=BEGIN
TestAllCallsByCodeunitId(CODEUNIT::”Implementation 1″);
TestAllCallsByCodeunitId(CODEUNIT::”Implementation 2″);
END;
}
CODE
{
LOCAL PROCEDURE TestAllCallsByCodeunitId@1(CodeunitId@1000 : Integer);
VAR
FunctionRef@1001 : Codeunit 50000;
BEGIN
FunctionRef.Create(CodeunitId, ‘TestOne’);
FunctionRef.Invoke;
FunctionRef.Create(CodeunitId, ‘TestTwo’);
FunctionRef.Invoke1Arg(1);
FunctionRef.Create(CodeunitId, ‘TestThree’);
FunctionRef.Invoke2Arg(5, 160101D);
END;
BEGIN
END.
}
}
While this is just a “nerdy” try to make NAV do something it can’t by default, maybe it will be interesting for someone.
I tried your code yesterday and it works BUT when i tried messing with parameters of type record for example things started to get complicated.
Another problem is byvar parameters also.
Great post – again!
I put all my votes on your interface suggestion. The issue I have with references is that they are “reflection-like” with the problems that follow such as no compile-time type checking and lower readability of code (just like code using RecordRef and FieldRef is a lot harder to read than “normal” code.)
Conceptually, interfaces are a lot easier to understand (and code) than events, and we would be able to adopt many proven object-oriented design patterns instead of needing to invent our own.
Imagine also the power interfaces could give when it comes to extensions: An extension could include an implementation of a given NAV interface, allowing an alternative implementation to be selected or configured through dependency injection.
Maybe interfaces do not need to be restricted to Codeunits. In NAV, we often have dual tables like Sales Header and Invoice Header. If both objects would implement an “Invoice” interface (basically specifying which fields are available), then this could be a very easy way to write more general code that works on any invoice (posted or not) and thereby avoid code duplication.
Yes, on a few more thoughts I also believe interfaces would be much better as they give the compile-time checking. Still, I wonder if any of these will be seriously considered by Microsoft 🙂
Where do we up-vote Interfaces? I feel like NAV already has everything they need in the back-end to do this and it really would be a simplistic change to the compiler. And it is the basis of nice C# polymorphism.
I too have been playing with many combinations of variant facades, broadcast patterns, blob serialisation, and reflection-style method invoking (“borrowing” code from yourself and Waldo as usual) and nothing is “nice”.
My dream is it would start with Codeunits, and end with a new object type called “Class” which could be linked to Records (i.e. the record is the interface/base class, the class is the code implementation on top – with overrides and all that jazz). I have a feeling that this will be somewhat confused/answered with the new Extension stuff…
Pingback: Changing NAV (C/AL) source code through C# | NAV Blog
Pingback: Codeunit interfaces in AL - Vjeko.com
Pingback: Codeunit interfaces in AL - Vjeko.com - Dynamics 365 Business Central/NAV User Group - Dynamics User Group
Pingback: Codeunit interfaces in AL - Microsoft Dynamics NAV Community
Pingback: Codeunit interfaces in AL | PA
Pingback: Codeunit Interfaces – this time for real! - Microsoft Dynamics NAV Community
Pingback: Harnessing Business Central’s Interface power with Discovery design pattern – _NavDrive
Pingback: Top 5 things I miss in AL - Vjeko.com
Pingback: Top 5 things I miss in AL - Vjeko.com - Dynamics 365 Business Central/NAV User Group - Dynamics User Group